Method - This is a way of finding one root of a quadratic(or cubic) equation, essentially by trial and error, but in a more ordered way.

In questions you are given a quadratic expression and told what numerical value it is equal to.

You are sometimes given that the value of 'x' lies between two numbers and asked that your answer be rounded to a particular number of decimal places.

You may wish to revise 'approximation' before proceeding.

Example - By using a 'trial & improvement' method find the positive value of x that satisfies the equation below.

'x' has a value between 1 and 2. Give your answer correct to one decimal place.

Move the number part of the equation to the right, leaving terms in 'x' on the left.

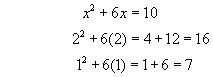
Remember we want the expression to equal 10. The value of the expression in the first instance comes to 16 , while in the second instance the value is 7.

Since (16 - 10 = 4) and (10 - 7 = 3) the value of x (to give 10) must be a number closer to x=1 than x=2.

So we try x=1.4

(1.5 is the average between 2 & 1, so we use 1.5 - 0.1 to give a bias towards the 1).

The value of x must be less than 1.4, since 1.4 gives 10.36(over 10).

Let's try x=1.35

The value of x must be greater than 1.35, since 1.35 gives 9.923(less than 10).

Let's try x=1.36

Since the value of x is to be rounded, the value of the expression in x is as close to 10 as is necessary.

So the value of x to satisfy the equation, (rounded to one decimal place) is 1.4

back to top