[ addition ][ subtraction ][ multiplication ][ division ][placing in order]

A fraction is made from two components: the numerator (on the top) and the denominator (on the bottom)

 numerator
denominator

Fraction Types:

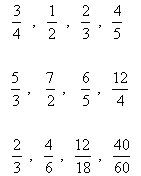
Fraction Addition - To add two fractions you must first find their common denominator. Then convert each to the new denominator and add the numerators.

Look at this example.

The common denominator is found by multiplying the two denominators together. In this case, multiply the 5 by the 3. This gives 15.

Now convert each factor to 15 ths by dividing the denominator of each into 15 and multiplying the result by each numerator.

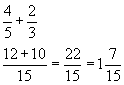
more examples...

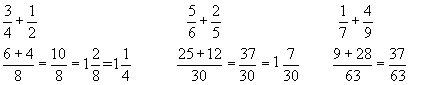
Fraction Subtraction - This is exactly the same as for addition except that the numbers above the common denominator are subtracted from eachother.

back to top

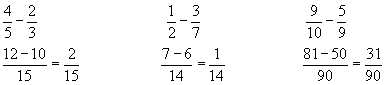
Fraction Multiplication - Here the numerators are multiplied along the top, while the denominators are multiplied along the bottom.

Fraction Division - The second fraction is turned upside down(inverted), the two fractions are multiplied together.

back to top

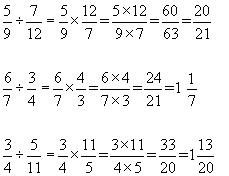
Placing fractions in order(ordering) - If a calculator is allowed in the exam paper, all you have to do is convert the fractions to decimals - divide each denominator into each numerator. However is a calculator is disallowed you must use the method shown below.

Simply find the common denominator of all the fractions(as with factor addition) and convert each fraction to the new denominator. Then order the fractions and cancel to get the original fractions.

The common denominator of all these fractions is 4 x 10 x 7 x 5 (=1400)

Dividing each denominator into this number and multiplying the answer by the respective numerator we get:

back to top