Simple Ratios - A ratio is a way of comparing the relative magnitude of different quantities.

A, B, C ..............20 : 30: 50

Simplification of Ratios - Division by common factors reduces the numbers used in a ratio. The ratio 20 : 30 : 50 becomes 2 : 3 : 5 .

examples:

20 : 55

4 : 11 (dividing by 5)

39 : 12

13 : 4 (dividing by 3)

56 : 24

7 : 3 (dividing by 8)

 

Dividing by Ratio - This is the method to follow:

• Add up the numbers of the ratio to give the total number of 'parts'.
• Make fractions of each ratio number divided by the number total.
• In turn, multiply each fraction by the number that is to be divided up.

Example #1 - Divide 90 in the ratio 3 : 2

total of ratio numbers = 3 + 2 = 5

 

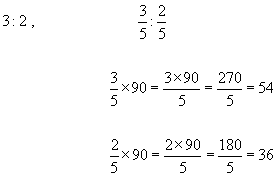
Therefore 90 shared in the ratio 3 : 2 is 54 and 36

 

back to top

------------------------------------------------------------------------------------------------------------

 

Example #2 - Divide 132 in the ratio 6 : 5

total of ratio numbers = 6 + 5 = 11

 

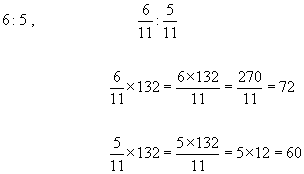
Therefore 132 shared in the ratio 6 : 5 is 72 and 60

------------------------------------------------------------------------------------------------------------

Example #3 - Divide 288 in the ratio 2 : 6 : 4

total of ratio numbers = 2 + 6 + 4 = 12

 

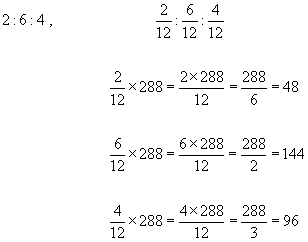
Therefore 288 shared in the ratio 2 : 6 : 4 is 48, 144 and 96

 

back to top

------------------------------------------------------------------------------------------------------------

Proportional Change is when a quantity is increased or decreased by multiplication with the numbers of a ratio expressed as a fraction.

The first number of the ratio becomes the numerator, while the second becomes the denominator.

Example #1 - increase 56 in the ratio 3 : 2

 

Example #2 - decrease 72 in the ratio 4 : 9

 

back to top

 

Contact GCSE Maths Tutor here - info@gcsemathstutor.com