Surds

Surds are mathematical expressions containing square roots. However, it must be emphasized that the square roots are 'irrational' i.e. they do not result in a whole number, a terminating decimal or a recurring decimal.

The rules governing surds are taken from the Laws of Indices.

rule #1

examples

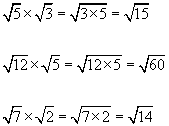
rule #2

examples

back to top

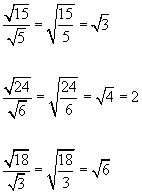
Some Useful Expressions

expression #1

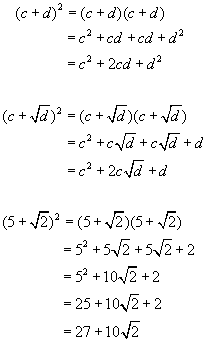
expression #2 - (the difference of two squares)

back to top

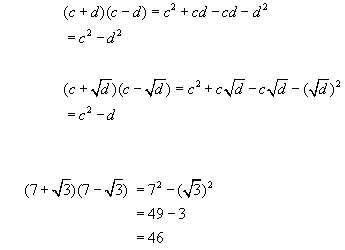
Rationalising Surds - This is a way of modifying surd expressions so that the square root is in the numerator of a fraction and not in the denominator.

The method is to multiply the top and bottom of the fraction by the square root.

back to top

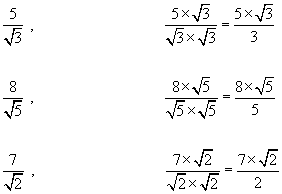
Rationalising expressions using the 'difference of two squares'

Remembering that : .... .....from 'useful expressions' above.

Example #1 - simplify

multiplying top and bottom by

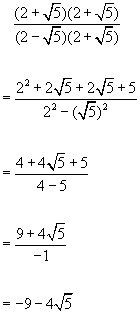
Example #2 - rationalise

multiply top and bottom by

back to top

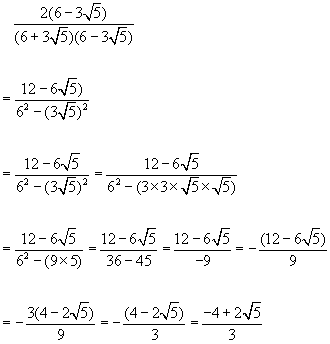
Reduction of Surds - This is a way of making the square root smaller by examining its squared factors and removing them.

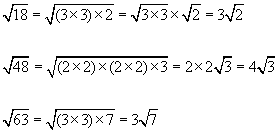
Rational and Irrational Numbers - In the test for rational and irrational numbers, if a surd has a square root in the numerator, while the denominator is '1' or some other number, then the number represented by the expression is 'irrational'.

examples of irrational surds: