line bisector

point to line

bisect angle

60 deg.angle

triangle

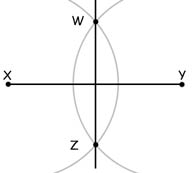
1. set the radius of your compass to more than than half the length of XY(but less than XY)

 

2. with centre X, draw an arc above and below the line XY

 

3. with centre Y, draw an arc above and below the line XY intersecting the arcs from X

 

4. the arcs intersect at points W and Z respectively above and below the line XY

 

5. join the points W and Z

 

6. the line WZ is the perpendicular bisector of XY

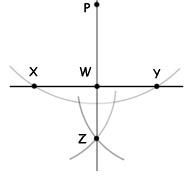
1. set the radius of your compass so that an arc with centre P cuts the line at two points

 

2. name these points of intersection X and Y

 

3. with the radius greater than half XY and centre X draw an arc below the line XY

 

4. repeat with centre Y

 

5. where the arcs intersect call point Z

 

6. the line joining Z to P is the perpendicular bisector of the line XY

 

7. where this line meets XY call point W

 

8. PW is the perpendicular from the point P to the line XY

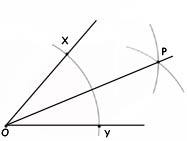
1. with centre O draw arcs to cut the arms of the angle at X and Y

 

2. using the same radius, from point X draw an arc between the arms of the angle

 

3. repeat at point Y

 

4. the two arcs intersect at point P

 

5. draw a line between P and O

 

6. PO is the bisector of the angle XOY

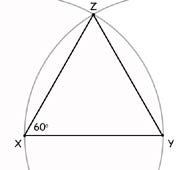
1. draw a line XY

 

2. with centre X and radius the length of the line, draw an arc above the line

 

3. repeat from centre Y

 

4. the point Z is where the arcs intersect

 

5. join XZ

 

6. join YZ

 

7. angle ZXY is a 60 deg. angle

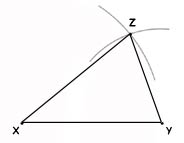
1. draw a line XY of given length, as the base to the triangle

 

2. with centre X and radius the length of the second side of the triangle, draw an arc above the line

 

3. with centre Y and radius the length of the third side of the triangle, draw an arc above the line

 

4. the point Z is where the arcs intersect

 

5. join XZ

 

6. join YZ