[ rounding to decimal places ][ rounding to tens, hundreds etc. ]

[ rounding to significant figures ][ estimates ][ bounds ]

Rounding to a required number of decimal places

The key is to look at the number after the required number of decimal places.

e.g. write 7.7186 to 3 decimal places(d.p.)

The 6 is what is called the 'decider'.

If this number is '5' or more, then the 3rd decimal is 'rounded up'.

Less than '5' and the decimal stays the same.

In this example 5.7186 becomes 5.719

The '8' is rounded up to '9', because '6' is 5 or more.

Examples

Rounding to tens, hundreds, thousands etc.

Examples

back to top

Rounding to a number of significant figures

The required number is found by ignoring any zeros infront or behind the line of numerals and rounding where needed.

Example #1

0.001292 ................to 3 significant figures

the three figures are 1 2 9

answer = 0.00129

Example #2

120,101 ................to 4 significant figures

the four figures are 1201

answer = 120,100

Example #3

13.27 ................to 3 significant figures

the 13.272 rounds up to 13.3

the three figures are 133

answer = 13.3

back to top

Estimates - An estimate is a rough approximation, usually of a calculation.

The rule is to round to one significant figure.

Example #1

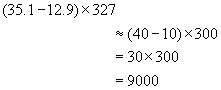
Example #2

back to top

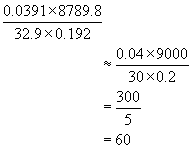
Upper & lower Bounds

The use of 'bounds' is a practical mathematical method quite different from 'decimal rounding'. Do not confuse the two. Decimal rounding depends on a '5 or more' being rounded up. Bounds is quite different.

Whenever measurements are expressed in the real world they are often given an upper bound(highest value) and a lower bound(lower value).

Example #1 - A length of wood is 1500 mm long, correct to the nearest 'm.m.'.

The upper bound is therefore: 1500.5 m.m.

The lower bound is therefore: 1499.5 m.m.

Note - The upper & lower bounds are HALF the degree of accuracy.

In our example, m.m., that is half of 1 m.m.

Example #2 - A poster measures 99.5 cm x 192.2 cm correct to the nearest 0.1 cm.

Find the upper and lower bounds for the poster's dimensions, hence find its maximum & minimum area.( to 2 d.p.)

upper bounds 99.55 , and 192.25................lower bounds 99.45 , 192.15

maximum area = 99.55 x 192.25 = 19138.488 = 19138.49 (2d.p.) sq. c.m.

minimum area = 99.45 x 192.15 = 19109.318 = 19109.32 (2 d.p.)sq. c.m.

back to top

Example #2 - A rocket travels a vertical distance of 50k.m.(correct to nearest k.m.) in 23.1 seconds(correct to the nearest 0.1 second.

What are the upper and lower limits to the rocket's average speed?

upper bounds 50.5k.m. , and 23.15 sec...........lower bounds 49.5k.m. , 23.05

The highest average speed is with the largest distance divided by the smallest time.

back to top