Home >> Number - Sequences
[ common difference sequences ][changing difference sequences]
Conventionally sequences have a first term or starting value, usually denoted by the letter 'a'.
The common difference 'd' is the difference between consecutive terms when the terms increase by a regular amount.
The difference change 'c' is the change between consecutive differences
The last term in a sequence of 'n' numbers is the nth term.
The general term is an expression in 'n' that can be used to calculate any term in the sequence.
'Common Difference' Sequences
The general term for term number 'n' , common diff. 'd' and first term 'a' is:
dn + (a - d)
e.g. : 4.....9.....14.....19.....24.....29.....
a = 4, d = 5
the nth term is dn + (a - d) = 5n + (4 - 5) = 5n - 1
n = 7 , 7th term is (5 x 7) - 1 = 34
------------------------------------------------------------------------------------------------------------
example #1 - Find the nth term in this sequence : 13, 20, 27, 34, 41, 48 ...
a = 13, d = 7
nth term = dn + (a - d) = 7n + (13 - 7) = 7n +6
------------------------------------------------------------------------------------------------------------
example #2 - Find the nth term in this sequence : 11, 19, 27, 35, 43, 51 ...
a = 11, d = 8
nth term = dn + (a - d) = 8n + (11 - 8) = 8n + 3
------------------------------------------------------------------------------------------------------------
example #3 - Find the nth term in this sequence : 9, 15, 21, 27, 33, 39 ...
a= 9, d= 6
nth term = dn + (a - d) = 6n + (9 - 6) = 6n + 3
------------------------------------------------------------------------------------------------------------
'Changing Difference' Sequences
The general term for term number 'n' , common diff. 'd' , first term 'a' and difference change 'c' is:
![]()
Example #1 - find the nth term of 3, 8, 14, 21, 29 ........
Writing the series with increases below:
![]()
remembering that the nth term is given by:
![]()
1st term, 'a' =3
first difference 'd' = 5
difference increase 'c' = 1
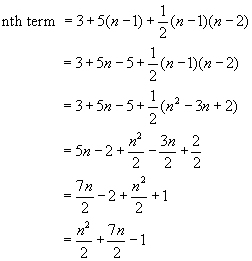
------------------------------------------------------------------------------------------------------------
Example #2 - find the nth term of 5, 7, 10, 14, 19 ........
Writing the series with increases below:
![]()
remembering that the nth term is given by:
![]()
1st term, 'a' =5
first difference 'd' = 2
difference increase 'c' = 1
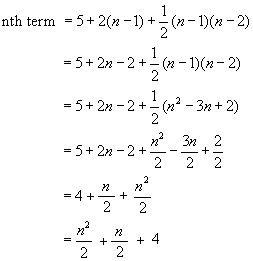
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
