Home >> Algebra - Quadratic Equations
Solution by factorising - This is best understood with an example.
solve:
![]()
You must first ask yourself which two factors when multiplied will give 12 ?
The factor pairs of 12 are : 1 x 12, 2 x 6 and 3 x 4
You must decide which of these factor pairs added or subtracted will give 7 ?
1 x 12 ...gives 13, 11
2 x 6 .....gives 8, 4
3 x 4 .....gives 7, 1
![]()
Which combination when multiplied makes +12 and which when added gives -7?
These are the choices:
(+3) (+4),
(-3) (+4),
(+3) (-4)
(-3) (-4) |
Clearly, (-3)(-4) are the two factors we want.
therefore
![]()
Now to solve the equation:
![]()
factorising, as above
![]()
either
![]()
or
![]()
for the equation to be true.
So the roots of the equation are: ![]()
Completing the square
This can be fraught with difficulty, especially if you only half understand what you are doing.
The method is to move the last term of the quadratic over to the right hand side of the equation and to add a number to both sides so that the left hand side can be factorised as the square of two terms.
e.g.
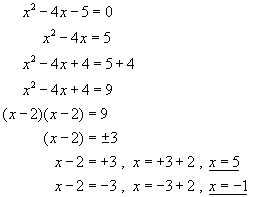
However, there is a much neater way of solving this type of problem, and that is by remembering to put the equation in the following form:
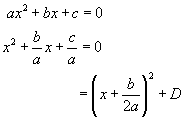
using the previous example,
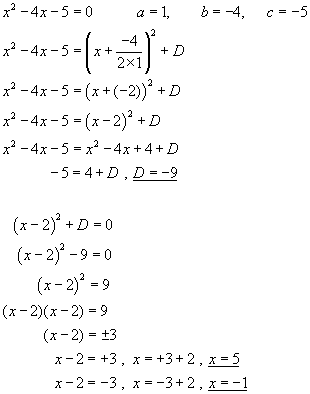
Using the Formula - the two solutions of quadratic equations in the form
![]()
are given by the formula:
![]()
Example Find the two values of x that satisfy the following quadratic equation:
![]()
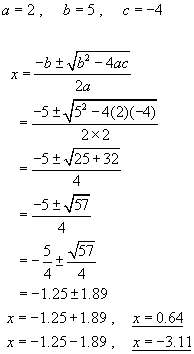
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
