the video & interactive library - everything at a glance

shape & space : circles
 

parts

subtended angles

 

 


  • a drop-down menu of resources for 'circles'

    • The parts of a circle

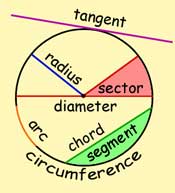
    circle parts

    centre - the point within the circle where the distance to points on the circumference is the same.

    radius - the distance from the centre to any point on the circle. The diameter is twice the radius.

    circumference(perimeter) - the distance around a circle.

    chord is a straight line joining two points on the circumference.

    diameter - a chord(of max. length) passing through the centre

    sector - a region enclosed by two radii and an arc.

    segment - the region enclosed by a chord and an arc of the circle.

    tangent - a straight line making contact at one point on the circumference, such that the radius from the centre is at right angles to the line.

    back to top

     

    GCSE Maths Tutor has free videos for many GCSE Maths topics

     

    Subtended angles

    When a chord subtends an angle on the circumference of a circle, the angle subtended at the centre of the circle is twice the angle.

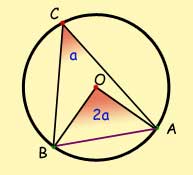
    circle - subtended angles #1

     

    A diameter subtends a right-angle at the circumference

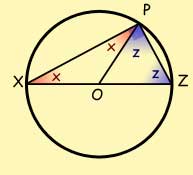
    90 deg. subtended angle

    angle XPZ = 90 deg.

    Angles subtended by a chord onto the circumference of a circle are equal.

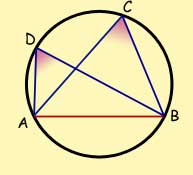
    subtended angles #2

    angle ADB = angle ACB

    back to top

     

    Learn GCSE Maths - use the GCSE Maths Forum to ask questions

     

    Chords

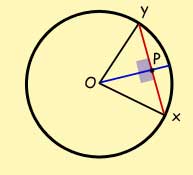
    chord #1

    The line joining the centre of a circle and the mid-point of a chord is perpendicular to the chord. The chord is bisected into two equal halves.

    XP = PY

    back to top

     

    Why not try out the new GCSE Maths interactive pages?

     

    Tangents

    circles - tangents

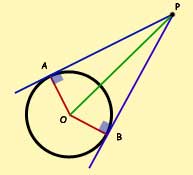
    The tangents to a circle from a point are equal in length.

    AP = BP

    also,

    the tangents subtend equal angles at the centre of the circle

    angle POA = angle POB

    and,

    the angles between the tangents and the line joining the centre of the circle and the point are equal.

    angle APO = angle BPO

    note : Triangle APO and triangle BPO are congruent.

     

    Contact GCSE Maths Tutor here - info@gcsemathstutor.com

     

    The angle between a tangent and a chord

    The angle between a tangent and a chord is equal to the angle subtended by the chord in the opposite segment.

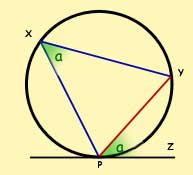
    circle - tangent #2

    angle ZPY = angle PXY

    back to top

     

    GCSE Maths revision from GCSE Maths Tutor

     

    Cyclic quadrilaterals

    Opposite angles in a cyclic quadrilateral add up to 180 deg.

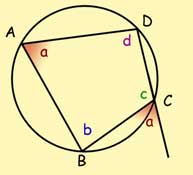
    circle - quads

    As with all quadrilaterals, the sum of the interior angles = 360 deg.

    Any exterior angle of a cyclic quadrilateral equals the interior opposite angle.

     

     

    back to top