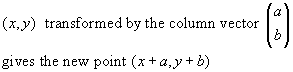the video & interactive library - everything at a glance

shape & space : transformations
 

points

 

 


  • a drop-down menu of resources for 'transformations'

    •  

     

    Translation of points

    A point (x,y) can be moved to another position by applying a column matrix vector.

    A column matrix vector is just two numbers, one above the other, surrounded by long brackets. The top number adds to the x-coordinate while the bottom number adds to the y-coordinate.

    vectors#2

    Example

    vector notation #2

    move right or left = x more positive or more negative
    move up or down = y more positive or more negative

    A(-1,1) to B(2,2) by going to the right 3 and up 1 by applying vector vector 3,1

    B(2,2) to C(1,-2) by going to the left 1 and down 4 by applying vector vector -1 -4

    C(1,-2) to D(-2,-1) by going to the left 3 and up 1 by applying vector vector -3,1

    back to top

     

    GCSE Maths ipod support for interactive maths - Safari browser required

     

    Translation of shapes

    This is similar to the translation of a point except that the vector column matrix is applied to each point of the shape in turn to move the whole shape to another position.

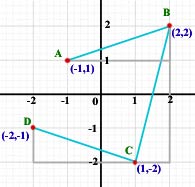
    example Translate the triangle ABC by the vector column matrix vector 3,-1

    vector notation #2

    Each x-coordinate is increased by 3 (moved right 3)

    Each y-coordinate is reduced by 1 (moved down 1)

    back to top

     

    Why not try out the new GCSE Maths interactive pages?

     

    Reflections

    A reflection is a mirror image of the shape about an arbitrary line. This line can be for example x=0(y-axis), y=3, y=x(diagonal) etc.

    Reflected points can be located by remembering that:

    each point is as far infront of the line as the image of the point is behind

    So measure the perpendicular distance of each point on the shape from the mirror line, then measure each distance the other side of the line to locate the points.

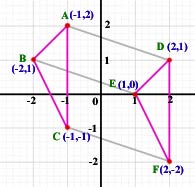
    Example Draw the reflection of triangle ABC in the y-axis.

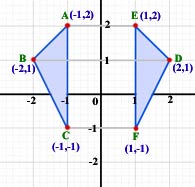
    vectors - reflection

    Point A is 1 unit infront of the y-axis mirror. Therefore the reflected point(E) is 1 unit the other side of the line.

    Similarly, B is 2 units infront. D is 2 units behind. C is 1 unit infront. F is 1 unit behind.

    Method for locating mirror images

    1. Use your set-square to draw perpendiculars from the 'mirror line' through each point of the shape
    2. Measure the point-'mirror line' distance for each point.
    3. Produce each line behind the mirror line the same distance to locate the mirrored points.

    back to top

     

    GCSE Maths Tutor has free videos for many GCSE Maths topics

     

    Rotations

    In order to rotate a shape, 3 pieces of information are required:

    the centre of rotation - the direction of rotation - the angle of rotation

    Example - Rotate triangle ABC through 60 deg. in a clockwise direction about point P.

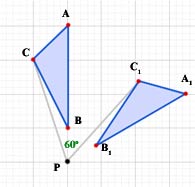
    transformations - rotation

    method

    1. draw a line PC between P and C
    2. measure the line PC
    3. draw a line 60 deg. clockwise from PC, centre P, the same length as PC
    4. repeat the method for B and A on the original shape
    5. finally join up the ends of the lines to make the original shape but rotated through 60 deg.

    back to top

     

    Learn GCSE Maths - use the GCSE Maths Forum to ask questions

     

    Enlargements

    In order to enlarge a shape, 2 pieces of information are required:

    the centre of enlargement - the scale factor

    Example Enlarge triangle ABC by a scale factor of 1.5 form the point P.

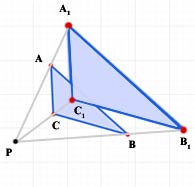
    transforms - enlargements

    method

    1. Draw a line through A, measuring 1.5 times PA.
    2. Draw a line through B, measuring 1.5 times PB.
    3. Draw a line from P through C, measuring 1.5 times PC.
    4. Join up the ends of the lines.

     

    Contact GCSE Maths Tutor here - info@gcsemathstutor.com

     

    back to top